Een vel A4 papier (of A3, A5, A6…) heeft als verhouding van de zijden 1 : √2. Deze eigenschap maakt dit papier geschikt voor wiskundige toepassingen. Katie Steckles (onderaan deze post) maakt in een plenaire lezing op de NWD van 2018 deze verhouding duidelijk, en ook dit voorbeeld van de vlieger komt voorbij.
In deze post behandelen we een eenvoudige toepassing van A4 papier, waarbij een aantal mooie wiskundige principes voorbij komen. De basis: neem een vel A4 papier.
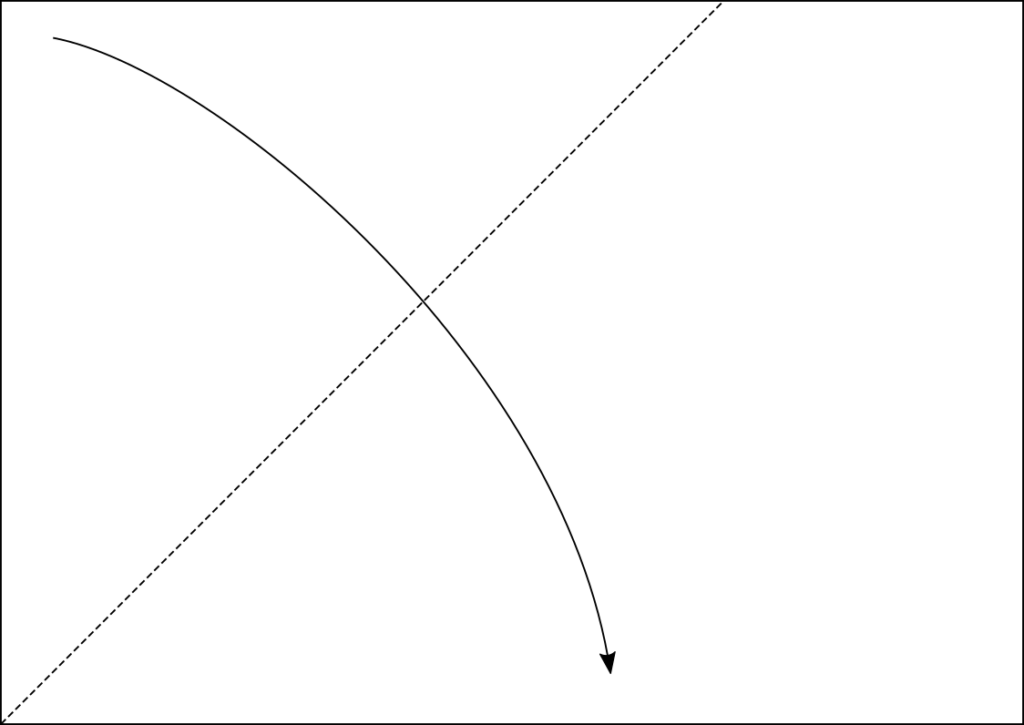
- Vouw de bissectrice van één van de hoeken.
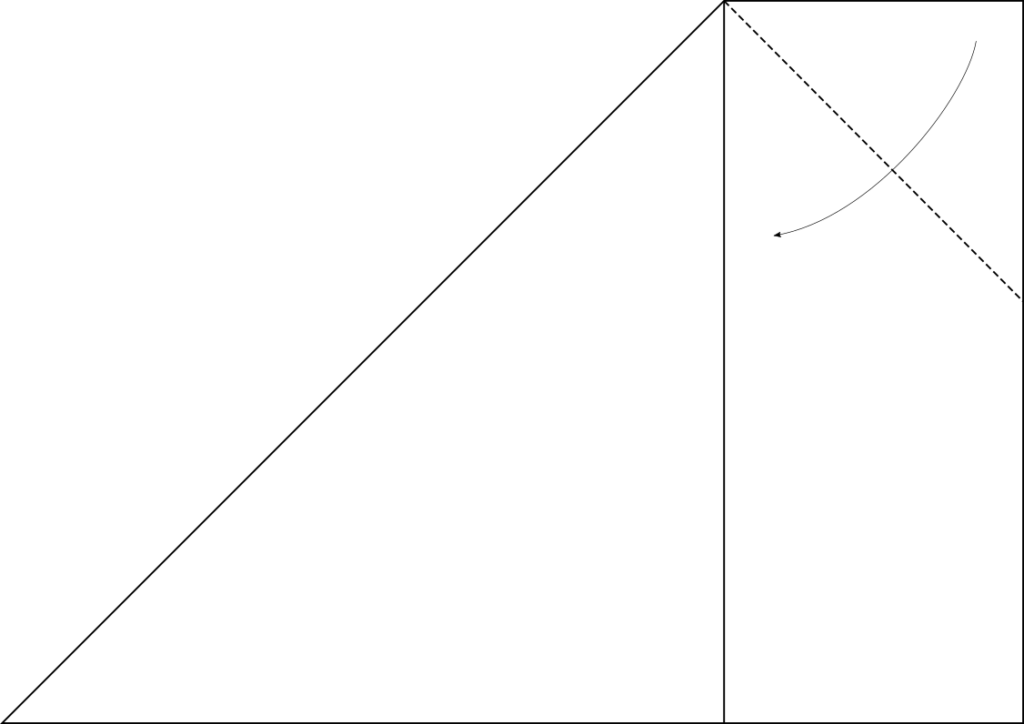
2. Vouw het restant van de lange zijde tegen de rand van de gevouwen hoek. Zorg dat de vouw aansluit bij de rand van de eerste vouw.
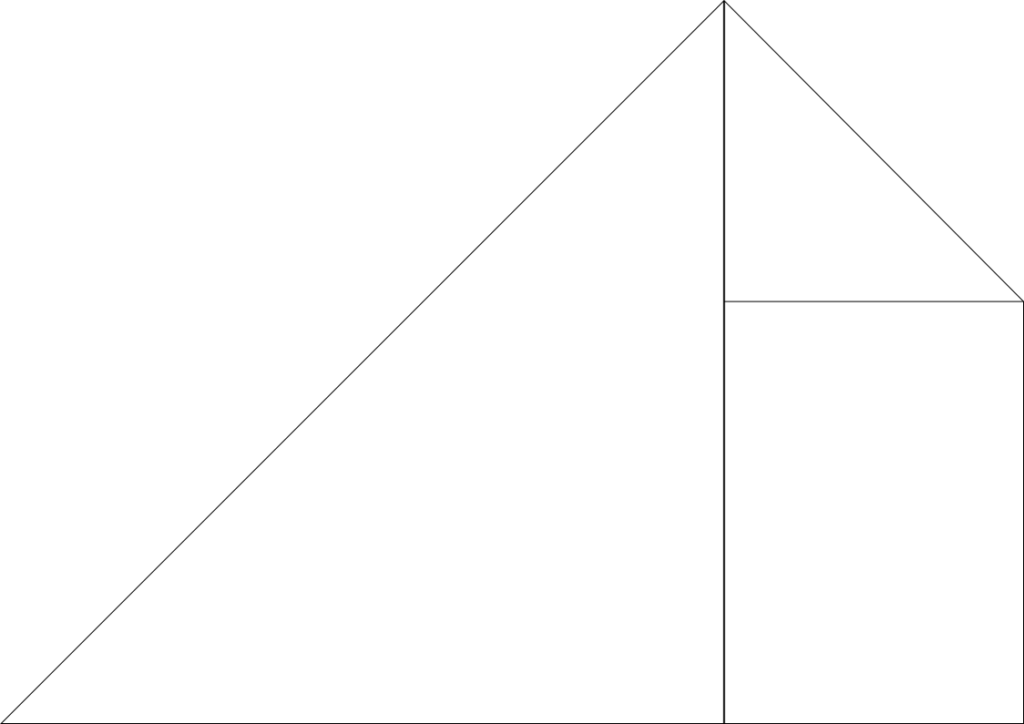
3. Als het goed is heb je nu dit figuur… en dat lijkt niet echt op een vlieger. Die zie je beter als je het papier omdraait!

4. Je kunt controleren of het écht om een vlieger gaat door te controleren of de figuur lijnsymmetrisch is… En? Klopt het? Hoe kan dit? Hieronder nog wat vragen om op te lossen. Neem daarbij 1 als lengte van de korte zijde van het A4 papier:
- Hoe lang zijn de zijdes van de vlieger?
- Wat is de oppervlakte van de vlieger?
Daar mag je even op puzzelen… antwoorden in de volgende post!
Het vouwen van de vlieger van A4papier zit ongeveer op 9 minuten in deze video, “The mathematics of paper”, van Katie Steckles, gemaakt op de NWD conferentie in 2018:
One thought to “Eenvoudige vlieger met mooie wiskunde”
Reacties zijn gesloten.