Uitwerking vlieger

In deze post de uitwerkingen van de vragen die gesteld zijn in de post over de mooie wiskunde van een eenvoudige vlieger.

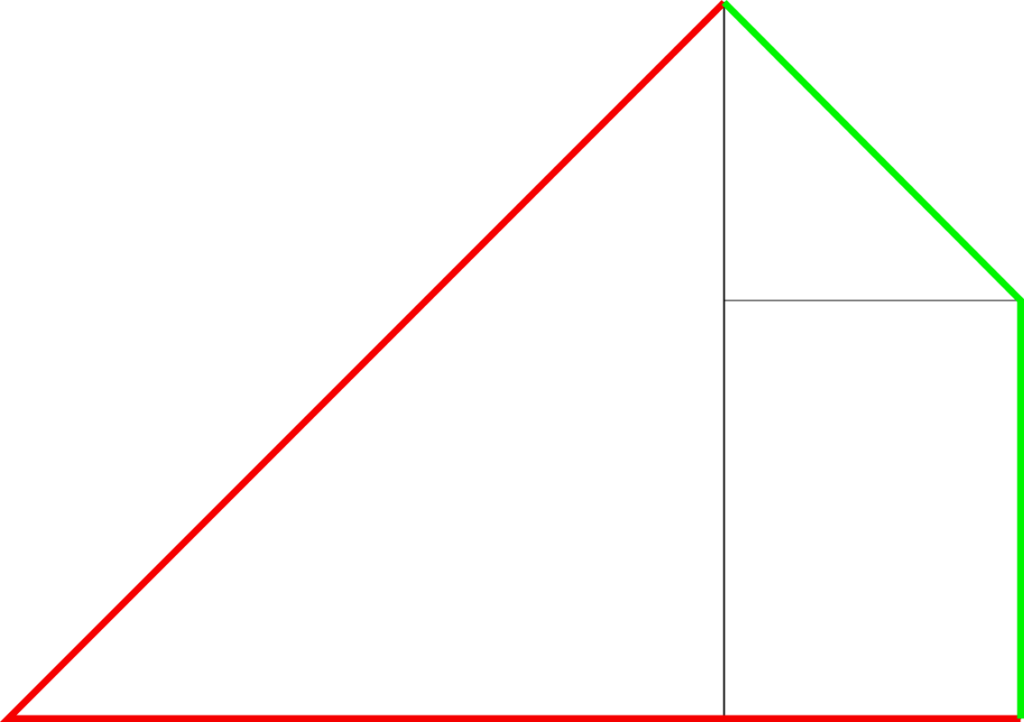
Lengte lange zijdes van de vlieger:

Als je de korte zijde van het A4 papier de lengte 1 geeft, dan is – op basis van de verhoudingen van A-formaat papier – de lange zijde √2. Als je de korte zijde omvouwt (waarmee je de grote driehoek krijgt), dan krijg je een gelijkbenige rechthoekige driehoek met hoeken van 45 – 45 en 90 graden, dus de verhouding 1:1:√2. Deze laatste verhouding volgt uit de stelling van Pythagoras. Ofwel: de lange zijde van de grote driehoek is √2. De rode zijdes van de vlieger uit het plaatje hierboven zijn dus even lang!

Lengte korte zijdes van de vlieger:

Schuine groene zijde rechtsboven: de rechte zijdes van de kleine rechthoekige driehoek rechtsboven hebben de lengte √2-1. Dat betekent dat de lange zijde de lengte √2(√2-1)=2-√2 heeft (reken eventueel na met de stelling van Pythagoras). Groene zijde rechtsonder: de hele zijde van het A4 papier heeft lengte 1, daar wordt een zijde van √2-1 van omgevouwen. Je houdt dan over: 1-(√2-1) = 2-√2, ofwel, ook de groene zijdes van de vlieger uit het plaatje hierboven zijn even lang!

Oppervlakte van de vlieger:

Om de oppervlakte van de vlieger te berekenen nemen we de oppervlakte van het hele vel papier (√2), min de oppervlakte van de twee omgevouwen driehoeken. Oppervlakte grote driehoek: 1/2. Oppervlakte kleine driehoek: 3/2- √2. Daarmee wordt de oppervlakte van de vlieger 2√2-2, ongeveer 0,83.

Je kunt de oppervlakte van de vlieger ook berekenen door gebruik te maken van de blauwe driehoek in de figuur hierboven. Deze blauwe driehoek is een halve vlieger. De onderzijde is √2, de rechterzijde is 2-√2. Ook hieruit volgt een totale oppervlakte van de vlieger van 2√2-2.